
1.数据特征类型
朴素贝叶斯的算法根据数据的类型可以分为两类,一类是样本属性特征值是离散型,第二类是属性特征值为连续型,下面我会基于两类模型来介绍这个算法。
1.属性是离散型,类的先验概率可以通过训练各类样本出现的次数来估计
2.属性是连续型,有两种方法,将连续属性范围值划分为各个离散区间,这种方法不太好控制区间的大小,不太实用。第二种方法是,可以假设连续变量服从某种概率分布,然后使用训练数据估计分布的参数,高斯分布通常被用来表示连续属性的类条件概率分布。
高斯分布有两个参数,均值和方差.
均值计算公式
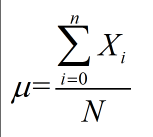 (公式1)
(公式1)
方差计算公式
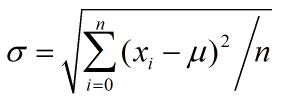 (公式2)
(公式2)
高斯分布概率密度函数
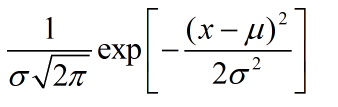 (公式3)
(公式3)
2.贝叶斯公式原型
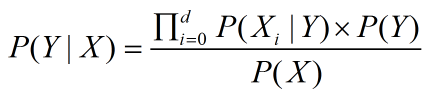 (公式4)
(公式4)
解释 d是每个X的属性个数,[x1,x2,x3,x4.....xd]每个属性,P(X)对于每个后验概率来说是固定不变的,所以,可以不计。
X实体属于Y分类的判断条件是根据Max[P(Yi|X)]来判断X实体属于哪个分类Y。
3.数据离散型贝叶斯使用例子
例子:概率模型:评分数据
评分数据
| 物品1 | 物品2 | 物品3 | 物品4 | 物品5 | |
|---|---|---|---|---|---|
| Alice | 1 | 3 | 3 | 2 | ? |
| 用户1 | 2 | 4 | 2 | 2 | 4 |
| 用户2 | 1 | 3 | 3 | 5 | 1 |
| 用户3 | 4 | 5 | 2 | 3 | 3 |
| 用户4 | 1 | 1 | 5 | 2 | 1 |
根据用户1到用户4的用户数据,来预测Alice对物品5的评分,这里可以使用贝叶斯模型,分别计算Alice对物品5评分为1,2,3,4,5的概率,其中概率最大的,则是Alice对物品5评分的最大可能性。
P(物品5=1|Alice)= P(Alice | 物品5=1) x P(物品5=1) = P(物品1=1 | 物品5=1) * P(物品2=3 | 物品5=1)* P(物品3=3 | 物品5=1)*P(物品4=2 | 物品5=1) * P(物品5=1)
= 1*1/2*1/2*1/2*1/2
P(物品5=2|Alice)= P(Alice | 物品5=2) x P(物品5=2) = P(物品1=1 | 物品5=2) * P(物品2=3 | 物品5=2)* P(物品3=3 | 物品5=2)*P(物品4=2 | 物品5=2) * P(物品5=2)
= 0*0*0*0*0
......................................
其他的物品以此类推,可以算出P(物品5=1|Alice)最大,则推测Alice用户对物品5的评分为1。
此例子是摘自《推荐系统》书中的一个例子
上面列子同理可用于文本分类模型中。用户看做文章,物品5评分看做文章的分类。同理可求出文章的所属的分类
4.数据连续型贝叶斯使用例子
判断车厘子和樱桃
车厘子与樱桃的鲜红值/直径、质量信息例子
| 水果类型 | 鲜红值 | 直径 | 质量 |
|---|---|---|---|
| 车厘子 | 0.81 | 1.02 | 8.85 |
| 车厘子 | 0.82 | 0.98 | 8.67 |
| 车厘子 | 0.78 | 0.99 | 8.75 |
| 车厘子 | 0.79 | 1.01 | 8.80 |
| 樱桃 | 0.56 | 0.85 | 7.32 |
| 樱桃 | 0.58 | 0.86 | 7.33 |
| 樱桃 | 0.59 | 0.83 | 7.29 |
| 樱桃 | 0.57 | 0.84 | 7.31 |
根据上表的数据,预测下表未知实体是樱桃还是车厘子
| 水果类型 | 鲜红值 | 直径 | 质量 |
| 未知 | 0.80 | 0.86 | 8 |
假设训练样本的特征满足高斯分布,则使用上面的公式1,公式2计算出均值和方差
根据计算公式,需要求出两种类型的水果的各个属性的均值和方差,计算结果如下:
各个属性的均值和方差
| 类型 | 鲜红值-均值 | 鲜红值-方差 | 直径-均值 | 直径-方差 | 质量-均值 | 质量-方差 |
|---|---|---|---|---|---|---|
| 车厘子 | 0.8 | 0.018257419 | 1 | 0.018257419 | 8.7675 | 0.076757193 |
| 樱桃 | 0.575 | 0.012909944 | 0.845 | 0.012909944 | 7.3125 | 0.0170778251 |
预测未知实体是车厘子还是樱桃,需要计算未知实体的属于车厘子和属于樱桃的后验概率谁大。
p(车厘子|unkown)=P(车厘子)*p(鲜红值|车厘子)*p(直径|车厘子)*p(质量|车厘子) / evidence
p(樱桃|unkown)=P(樱桃)*p(鲜红值|樱桃)*p(直径|樱桃)*p(质量|樱桃) / evidence
默认 P(车厘子)和P(樱桃)为1/2。evidence为常数,通常用来对各类的后验概率之和进行归一化。
evidence=P(车厘子)*p(鲜红值|车厘子)*p(直径|车厘子)*p(质量|车厘子)+P(樱桃)*p(鲜红值|樱桃)*p(直径|樱桃)*p(质量|樱桃);
概率密度求解
p(鲜红值|樱桃)可通过 公式3 来计算,均值和方差,分别带入 樱桃 的鲜红值得均值和方差,求出高斯分布概率密度,其他属性,以此类推。
最后根据计算结果来看,未知实体属于樱桃还是车厘子的概率大。
spark demo
朴素贝叶斯Spark MLib实现